Megan Langford

Triangles have several different types of centers that are constructed in various ways. Today, we will focus on comparing centroids and circumcenters of triangles.

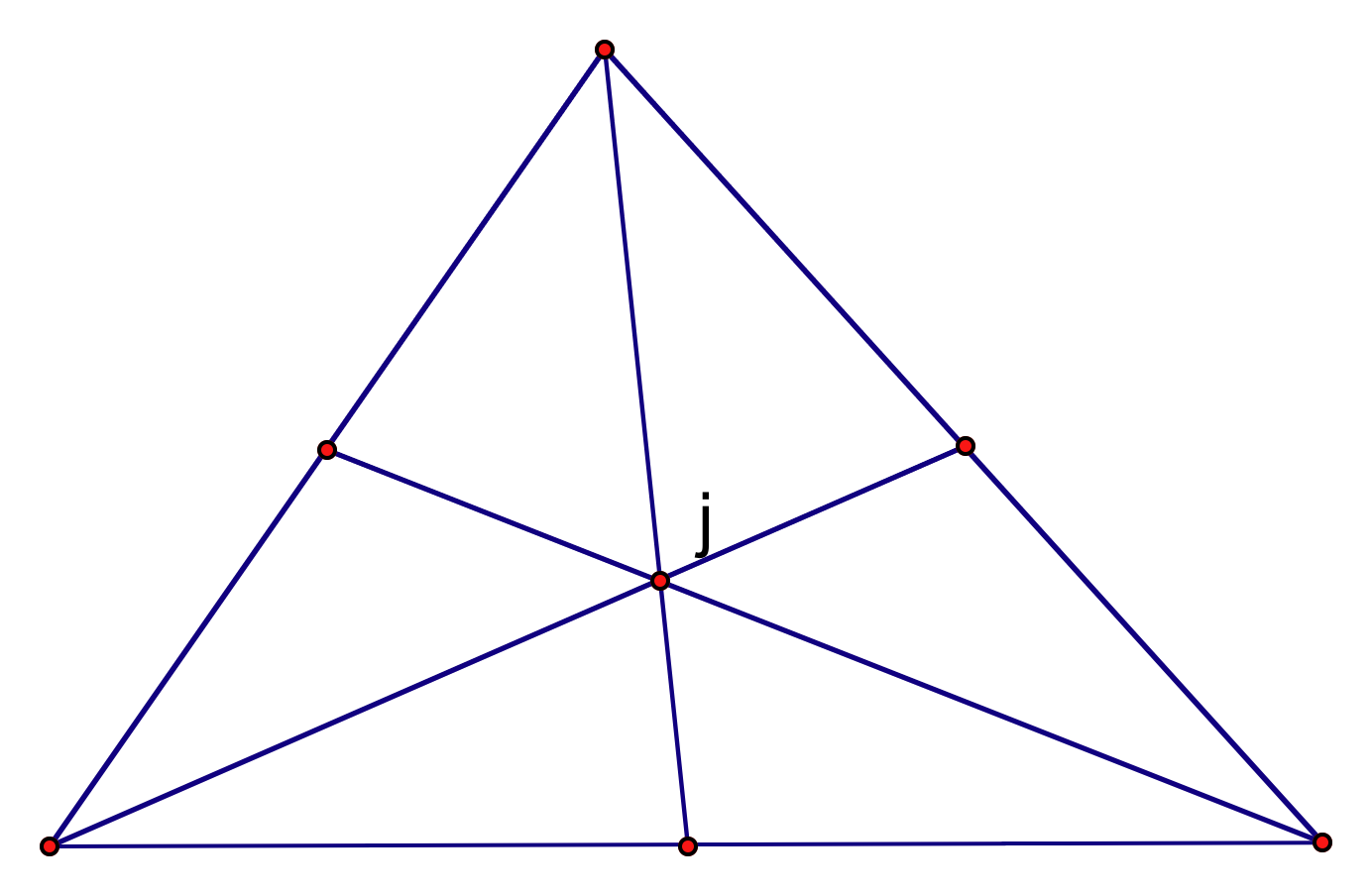
A centroid is constructed by obtaining the intersection of the three medians of a triangle. The medians are created by the line segments between each vertex and the midpoint of its opposite side.

Let us construct a triangle to illustrate this concept using Geometer’s Sketchpad. First, we will create a triangle. Next, we will take the midpoint of each side. Then we will create the medians of the triangle by drawing line segments to connect each vertex with its opposing side’s midpoint. Finally, we will label the intersection of these medians (the centroid) with a j. Our picture will appear as follows:

Now, let’s explore where the centroid would lie on several different shapes of triangles.

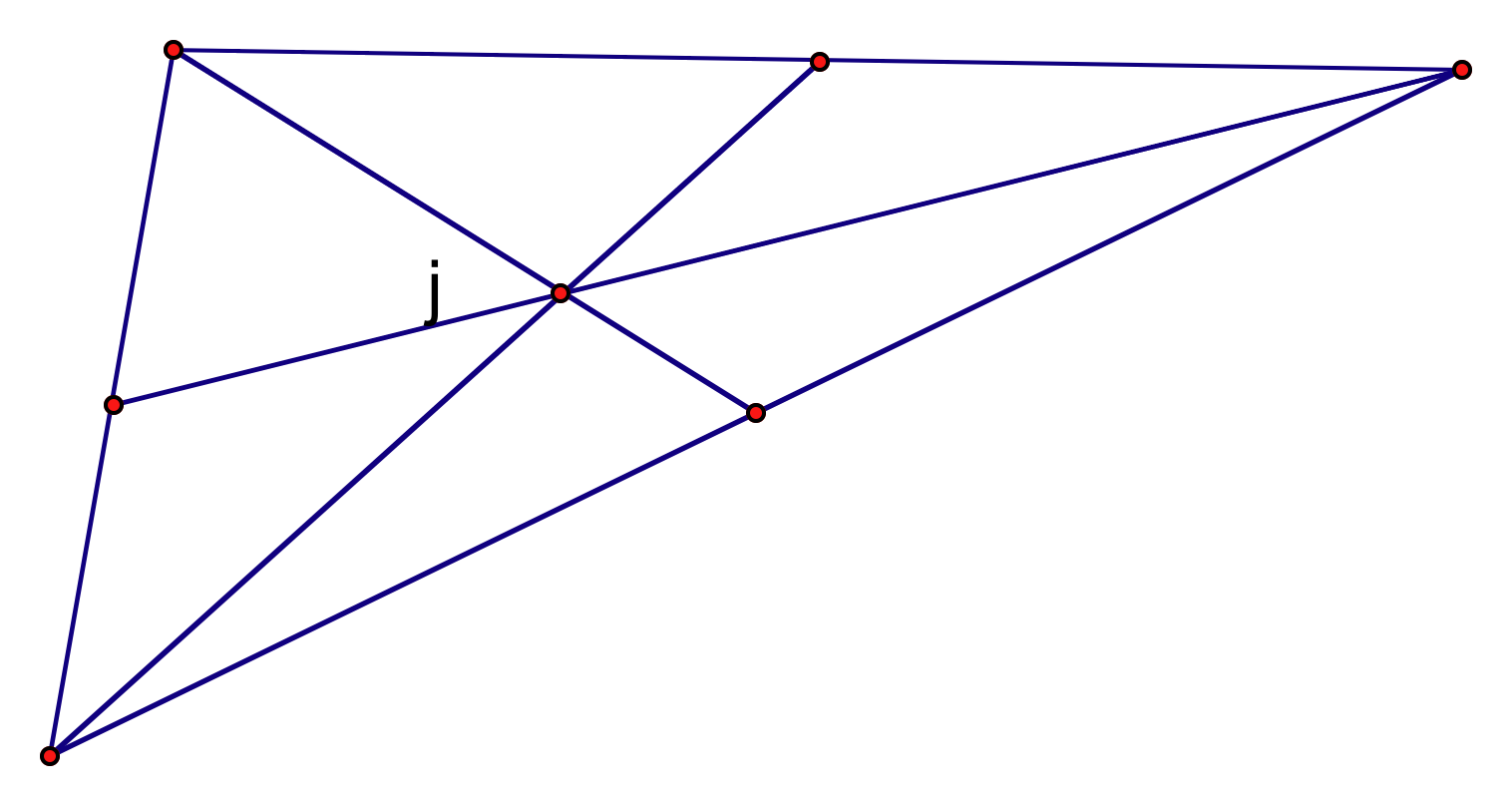
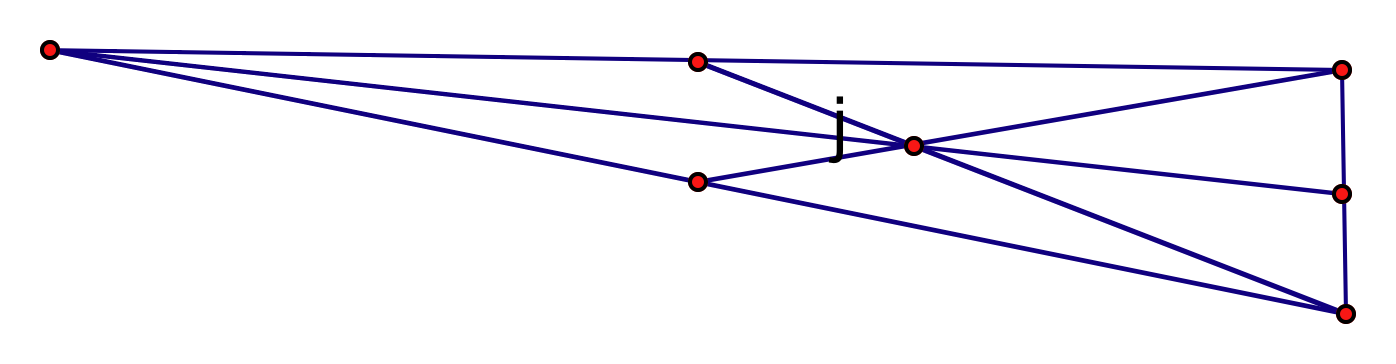
If we consider the centroid to be the center of gravity of a triangle, we begin to understand why its location ends up being where it is in any given triangle. Consider the situation where we take a paper cut-out of any of the above triangles. If we then try to balance the paper triangles on just one of our fingertips, then the centroid would be the point where we would find the balance for the triangle not to fall off of a fingertip.

This leads us to our primary observation about the location of the centroid for various triangles. The most obvious fact is that the centroid never leaves the bounds of the triangle. This makes sense both practically and mathematically. This makes sense practically because of course the balance point of a paper triangle not to fall off a fingertip would never exist outside of the triangle itself. If it did, the triangle would fall to the ground right away, so this could not occur. Mathematically, we realize that the centroid could never be located outside of the triangle itself because it was constructed by obtaining the intersection between each side’s midpoint and its opposing vertex. There is no possible way these lines would intersect only outside of the triangle itself, simply due to the nature of the construction.

Next, we will discuss circumcenters of triangles.

In order to create a circumcenter and circumcircle, we will first construct a triangle. We will then create a circle using the vertices of the triangle to lie along the perimeter of the circle. Next, let’s find the midpoints for each side of the triangle. For each midpoint, we will then construct the line perpendicular to that side of the triangle that passes through the given midpoint. Where these three lines perpendicular to the sides intersect, this is our circumcircle.

We know this is true because the circumcenter is the point equidistant from the three vertices of the triangle. Since we know that a point equidistant to two of the vertices lies on the perpendicular bisector of the segment determined by the two vertices, the circumcenter will lie along each of the lines we create in this manner. Therefore, our circumcenter is located at the intersection of the perpendicular bisectors of each side of the triangle.

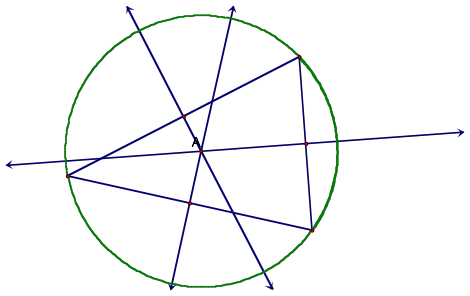
Of course, we have labeled the circumcenter of the triangle with an A. Let us go ahead and take a look at what happens to the circumcenter as we modify the shape of the triangle.

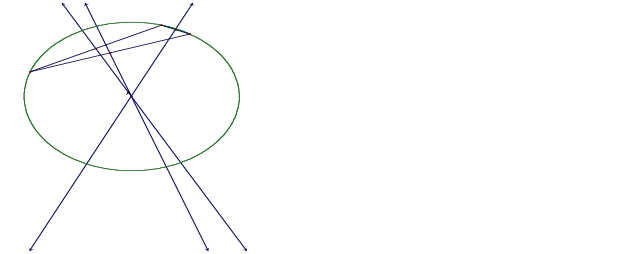
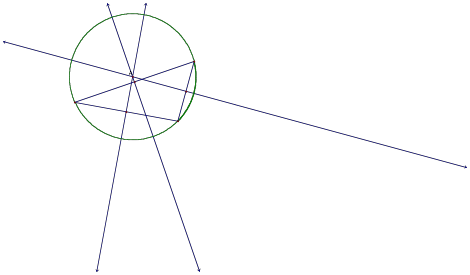
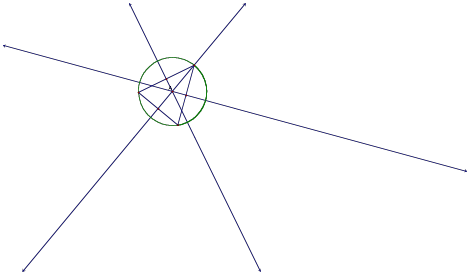
We can now observe the behavior patterns of the circumcenter as we change the shape of the triangle from which it was created. Through our various triangle shapes, we can notice that the most obvious difference between the circumcenter and the centroid is that while the centroid always appears inside the triangle, the circumcenter has the ability to exist well outside of the bounds of the original triangle. However, it is also possible that the circumcenter is located inside or on an edge of the original triangle.

Since the circumcenter is constructed by obtaining perpendicular bisectors of each side of the triangle, its location is more affected by the angles created by those sides. No area is really off limit as a possible location of a circumcenter, since we can move it anywhere by simply modifying the angles created by the sides of the triangle.